Article of Talal Uddin
Final destination of the equation of a curve
একটি বক্ররেখার সমীকরণের শেষ গন্তব্য – তালাল উদ্দিন
[সার কথাঃ আমি কোন গণিতবিদ নই। অনেকটা খেয়ালের বশে লেখাটির সূত্রপাত। তাই কতগুলো সরল ধারণার ওপর ভিত্তি করে প্রবন্ধটির গোড়াপত্তন হয়েছে। আমরা সবাই জানি যে, জীবন পুষ্পশয্যা নহে। জীবনকে তাই এখানে বক্ররেখার সাথে তুলনা করা হয়েছে। আর সাহিত্যের ভাষায় গাণিতিক সমীকরণ ব্যবহার করে এ ধারণাটির প্রতিপাদন করা হয়েছে। আপনি তাই এটাকে গণিতের সাহিত্য বলতে পারেন। বক্ররেখাটির সমীকরণের ফলাফল হল শূন্য। যেটা মানুষের মৃত্যুকে নির্দেশ করে। কেননা মৃত্যুর পরে মানুষের সকল পার্থিব অর্জন বিগ জিরো হয়ে যায়। পেছনে পড়ে থাকে তার বাড়ি, গাড়ি, সহায় সম্পত্তি ইত্যাদি । অন্ধকার অঞ্চল মানুষের জীবনের কঠিন সময়গুলোকে নির্দেশ করে যা সে উতরিয়ে ওঠতে সক্ষম হয় (যদিও অনেকেই সক্ষম হয় না। সরলীকরণের অংশ হিসেবে ধরে নেওয়া হয়েছে।যেহেতু মানুষ সৃষ্টির সেরা জীব)। মানুষের জীবনের সর্বোচ্চ অর্জনের মানকে খুব বেশি ধরা হয়নি। কেননা মানুষ তার সম্ভাবনার খুব কম অংশই বাস্তবে প্রতিফলিত করতে পারে।]
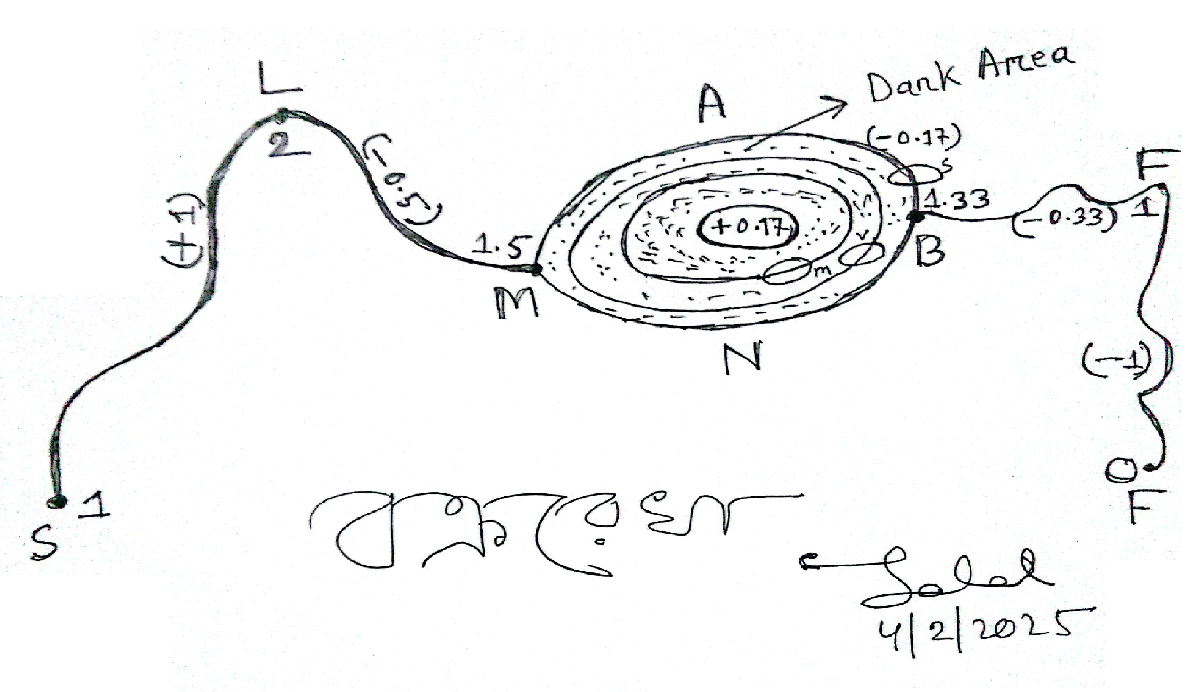
ক্রমাগত দিক পরিবর্তনশীল একটি বক্ররেখার ক্ষেত্রে বলা যায়,
S.L + M.B+ F.F = 0
Assumed Value:
S=19, L=12, M=13, B=2, F=6, F=6
সাধারণ গণিতে প্রমাণঃ
S.L + M.B + F.F = 0
বা, 19×12 + 13×2 + 6×6 =0
বা, 228+26+36 =0
বা, 290=0
বা, 2 + 9+ 0=0
বা, 11=0
বা, 1 + 1=0
বা, 2 = 0
চিত্র হতে প্রমাণ:
গুণনবিধি অনুসরণ করে,
S.L= 1 × 2= 2
M.B= 1.5 × 1.33 = 2
F.F= 0 × 1= 0
L.H.S
S.L+ M.B+ F.F
=2+2+0
=0+0+0 [ যেহেতু 2=0]
=0
=R.H.S
বিস্তারিত আলোচনাঃ
Let,
The highest attainable value = + 1
Middle value = 0
Highest forgoing value = -1
১ম পর্যায়ঃ
মনে করি, একটি বক্ররেখা S থেকে যাত্রা শুরু করে L বিন্দুতে এসে থেমে যায়। L বিন্দু হচ্ছে রেখাটির সর্বোচ্চ বিন্দু যেটা সমস্ত রেখার উপর প্রভাব বিস্তারের ক্ষমতা রাখে। যেহেতু এখানে সর্বোচ্চ মান অর্জিত হয়েছে। চিত্রানুসারে, S.L = +1.
২য় পর্যায়ঃ
এখন বক্ররেখাটি L বিন্দু থেকে নিচে নেমে M বিন্দুতে এসে থামে। এতে তার মান কিছুটা কমে যেতে থাকে।
চিত্রানুসারে, L.M = -0.50.
৩য় পর্যায়ঃ রেখাটি যখন M বিন্দুতে এসে থামে তখন সে দ্বিধাদ্বন্দ্বে ভুগে যে, সে B বিন্দুতে কেমন করে যাবে। তখন সে সৌর মডেলের মতো পথ করে মূল কেন্দ্রে (+0.17) মান নিয়ে বিভিন্ন গ্রহ যেমন বুধ, শুক্র ও শনির বাধা পেরিয়ে আসতে থাকে। এখানে বুধ, শুক্র ও শনিকে M, V ও S দ্বারা প্রকাশ করা হয়। এ দীর্ঘ পথযাত্রায় সে প্রচুর শক্তি হারাতে থাকে এবং পূর্বের অবস্থানের মান থেকে কেন্দ্রের মানের সমমান হারিয়ে (অর্থাৎ -0.17) B বিন্দুতে এসে থামে। এভাবে সে সাম্যাবস্থায় পৌঁছায়। এ সৌর মডেলের পথটিকে ABMN নামে চিহ্নিত করা যায়। সৌর মডেলের পথ বলা হলে ও বাস্তব জীবনের সাথে মিল রেখে এটিকে অন্ধকার অঞ্চল হিসেবে ভূষিত করা যায়। অনেকটা পদার্থ বিজ্ঞানের ডার্ক মেটার বা ডার্ক এনার্জির মতো। তাই এখানে M.B = 0 হবে।
[ যেহেতু, Middle value = 0] কিন্তু উপরের আলোচনায় বলা হয়েছে যে, M বিন্দু থেকে B বিন্দুতে পৌঁছতে রেখাটি কেন্দ্রের মানের সমপরিমাণ মান (0.17) হারায় । তাই শুধু এ মানটি বাদ যাবে। এটাকে অন্ধকার অঞ্চলের মান বলে অভিহিত করা যেতে পারে। যেমন আমরা অতীতের কোন খারাপ স্মৃতি বা খারাপ কোন অভিজ্ঞতাকে হৃদয় থেকে মুছে দিতে চাই।
ফুটনোট: শনি গ্রহের বিশেষত্ব হল এখানে এসেই রেখাটি তার কেন্দ্রের পজিটিভ মান হারিয়ে ফেলবে এবং মাইনাস মান ধারণ করবে। কেননা এটি কেন্দ্র থেকে বহু দূরে অবস্থিত।।
৪র্থ পর্যায়ঃ
যখন রেখাটি B বিন্দু থেকে F বিন্দুতে এসে থামে তখন তার মান কমে যেতে থাকে। চিত্রানুসারে,
B.F = – 0.33
শেষ পর্যায়ঃ
যখন রেখাটি F বিন্দু থেকে F বিন্দুতে নামে তখন সে সর্বোচ্চ মান হারাতে থাকে। চিত্রানুসারে, F.F = – 1.
এখন,
S.L + L.M + M.B + B.F + F.F
= +1 + (-0.50) + 0 + (0.33)+ (-1)
=1- 0.50 + 0 – 0.33 – 1
= – 0.83
S.L + L.M + M.B + B.F + F.F = -0.83________(1)
আবার,
L.M + B.F
= – 0.50 + ( – 0.33)
= – 0.50 – 0.33
= – 0.83
L.M + B.F = – 0.83________(2)
By substracting from equation (1) to (2) we get, S.L + M.B+ F.F = 0
[Proved]
পরিশেষে বলা যায়, জীবনের এ দীর্ঘ যাত্রাকে একটি রেখা দিয়ে সরলীকরণ করা যায় না। তাই এটাকে চূড়ান্ত কিছু ভাবা ভুল হবে। এটা ছিল শুধুমাত্র ক্ষুদ্র একটি প্রয়াস। লেখক এবং নাট্যকার শোলম আলেইচেমের একটি উক্তি দিয়ে শেষ করতে চাই। “জীবন জ্ঞানীদের জন্য একটি স্বপ্ন, বোকাদের জন্য একটি খেলা, ধনীদের জন্য একটি কৌতুক, দরিদ্রদের জন্য একটি ট্র্যাজেডি।” আমার জন্য একটি স্বপ্ন। আপনারটা আপনি চিনে নিবেন। আর সে মতে রেখা অঙ্কন করবেন।।
তালাল উদ্দিন | Talal Uddin
New Bengali Story 2023 | করিমের একদিন | তালাল উদ্দিন
New Bengali Story 2023 | তুতানের পৃথিবী | গল্পগুচ্ছ
New Bengali Story 2023 | আশার আলো | সুভাষ নারায়ন বসু
New Bengali Article 2023 | কবিতার অন্তরাত্মা
Shabdodweep Web Magazine | Final destination of the equation of a curve | Talal Uddin
Mathematics is a fascinating subject that guides us through various aspects of life. Among its many concepts, the equation of a curve holds a significant place. It helps in understanding the shape, movement, and final behavior of a curve. But what exactly is the final destination of the equation of a curve?
Understanding the Equation of a Curve
An equation of a curve is a mathematical representation of a curve in a coordinate system. It defines how a curve behaves and how its points are positioned in a given space. Curves can be linear, parabolic, circular, or even complex, depending on their equations. Understanding the equation of the curve helps in multiple fields, such as physics, engineering, and even art.
The Journey of a Curve in Mathematics
Just like a river flowing towards the sea, a mathematical curve also has a destination. This destination is often determined by the behavior of the equation. If we study the limits and asymptotes, we can predict where the curve will finally settle. In mathematical terms, this is known as the final destination of the equation of a curve. Some curves may end at infinity, while others may stabilize at a particular point.
For example, if we take the simple equation of a straight line, such as y = mx + c, its destination is infinite in both directions. However, for a parabola given by y = ax² + bx + c, the final destination depends on the direction in which it opens. Similarly, complex curves like logarithmic or trigonometric functions may oscillate indefinitely or settle at a particular limit.
Final Destination of the Equation of a Curve in Real Life
Mathematics is not just numbers; it is also philosophy. When we talk about the final destination of the equation of a curve, it resembles life itself. Life, like a curve, has its own equation with different factors influencing its direction. Just like how an equation determines the shape of a curve, our choices, surroundings, and fate shape our life’s journey.
Mathematical Interpretation of Life’s Final Destination
If we analyze human life mathematically, it resembles a complex curve rather than a straight line. Some phases of life resemble exponential growth, while others resemble decline. Just like the equation of a curve, human life has critical points, turning points, and inflection points. Some lives reach a stable final destination, while others continue their journey infinitely.
Just like in mathematics, where the final destination of the equation of a curve is determined by initial conditions and external forces, life’s destination is shaped by fate and human effort. Whether in mathematics or philosophy, every journey has an endpoint, a final resting place where everything becomes clear.
Conclusion
The final destination of the equation of a curve is a mathematical concept with deeper meanings beyond numbers. It describes the endpoint of a curve in a coordinate plane but can also symbolize the final purpose of human life. The equation of the curve helps in understanding not just geometry but also the philosophical aspects of existence.
By connecting mathematics with philosophy, we realize that every curve, every life, and every path has a purpose. Understanding this equation helps us navigate through both numbers and emotions, leading us to our final destination.